Bài toán tiếng Anh về đếm hình chữ nhật
Bài toán do Việt Nam đề nghị và được chọn làm đề thi đồng đội lớp 6 tại cuộc thi Toán học trẻ quốc tế Indonesia 2011 (IIMC 2011).
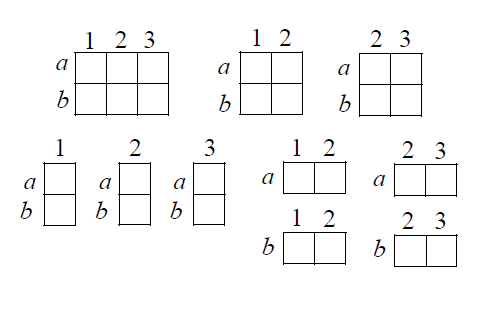


Ta sẽ giải bài toán bằng phương pháp phần bù tập hợp.
Bước 1: Tính toàn bộ số hình chữ nhật tạo thành.
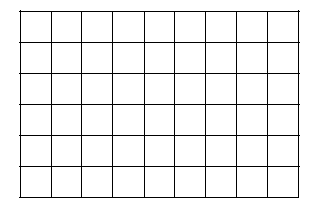
Hình chữ nhật 6 x 9 gồm có 7 đường thẳng nằm ngang song song với nhau và có 10 đường thẳng đứng song song với nhau.
Mọi hình chữ nhật bất kỳ đều là giao của 2 đường thẳng nằm ngang với 2 đường thẳng đứng.
Chọn cặp 2 đường (a; b) nằm ngang có: (7 x 6) : 2 = 21 (cách).
Chọn cặp 2 đường (c; d) thẳng đứng có: (10 x 9) : 2 = 45 (cách).
Vậy số hình chữ nhật tạo thành là: 21 x 45 = 945 (hình). (1)
Bước 2: Tính số hình chữ nhật có diện tích là một số lẻ.
Các hình chữ nhật có diện tích lẻ là giao của các cặp đường nằm ngang có khoảng cách lẻ với các cặp đường thẳng đứng có khoảng cách lẻ.
Số cách chọn cặp đường (a; b) nằm ngang có khoảng cách 1, 3, 5 lần lượt là 6, 4, 2 nên có 6 + 4 + 2 = 12 cách chọn cặp đường nằm ngang có khoảng cách lẻ.
Số cách chọn cặp đường (c; d) thẳng đứng có khoảng cách 1, 3, 5, 7, 9 lần lượt là 9, 7, 5, 3, 1 nên có 9 + 7 + 5 + 3 + 1 = 25 cách chọn cặp đường thẳng đứng có khoảng cách lẻ.
Số các hình chữ nhật có diện tích lẻ là: 12 x 25 = 300 (hình). (2)
Bước 3: Tính số hình chữ nhật có diện tích là một số chẵn.
Từ (1) và (2) suy ra số các hình chữ nhật chứa một số chẵn các ô vuông đơn vị là: 945 − 300 = 645 (hình).
Đáp số: 645.
We will solve this problem by finding the complement of a set.
Step 1: Find the total number of rectangles in a 6 × 9 table.
In a 6 x 9 table, there are 7 parallel horizontal lines and 10 parallel vertical lines.
A rectangle is made up of 2 parallel horizontal lines and 2 parallel vertical lines.
There are (7 x 6) : 2 = 21 ways to select a pair of horizontal lines (a; b).
There are (10 x 9) : 2 = 45 ways to select a pair of parallel vertical lines (c; d).
Thus, the total number of rectangles in a 6 ´ 9 table is: 21 ´ 45 = 945 (rectangles). (1)
Step 2. Find the number of rectangles whose area is an odd number.
A rectangle whose area is an odd number is made up of two parallel horizontal lines whose distance from each other is odd and two parallel vertical lines whose distance from each other is odd.
There are 6, 4, 2 ways to select a pair of horizontal lines (a; b) whose distance from each other is 1, 3, 5 respectively. So there are 6 + 4 + 2 = 12 ways to select a pair of vertical lines with odd length.
There are 9, 7, 5, 3, 1 ways to select a pair of vertical lines (c; d) whose distance from each other is 1, 3, 5, 7, 9 respectively. So there are 9 + 7 + 5 + 3 + 1 = 25 ways to select a pair of horizontal lines with odd length.
Thus, the number of rectangles whose area is an odd number is: 12 x 25 = 300 (rectangles). (2)
Step 3: Find the number of rectangles whose area is an even number.
From (1) and (2), it follows that the number of rectangles which consist of an even number of unit squares is 945 − 300 = 645 (rectangles).
The answer is 645.
| Consist of: bao gồm | Horizontal: nằm ngang |
| Unit square: ô vuông đơn vị | Vertical: thẳng đứng |
| Odd/even: lẻ/chẵn | Be made up of: được tạo thành bởi |
| Set: tập hợp | Distance: khoảng cách |
| Complement: phần bù (tập hợp) | Respectively: tương ứng |
| Parallel: song song | It follows that: suy ra |






KẾT QUẢ VÒNG CHUNG KẾT KỲ THI TÌM KIẾM TÀI NĂNG TOÁN HỌC QUỐC TẾ ITMC 2022
Ban Tổ chức ITMC xin thông báo và chúc mừng các Thí sinh Vòng Chung kết Kỳ thi Tìm kiếm Tài năng Toán học Quốc tế ITMC 2022 đã xuất sắc đạt được những thành tích vô cùng đáng tự hào, mang lại vinh quang cho Đội tuyển học sinh giỏi Việt Nam tại ITMC 2022.
ĐỘI TUYỂN HỌC SINH GIỎI VIỆT NAM THAM DỰ VÒNG CHUNG KẾT ITMC 2022
Ngày 20/02/2022, Đội tuyển học sinh giỏi Việt Nam tham dự "Kỳ thi Tìm kiếm Tài năng Toán học Quốc tế ITMC 2022" đã hoàn thành phần tranh tài của mình cùng các thí sinh Quốc tế.
GMaths xây dựng niềm tin từ tâm huyết, chất lượng đội ngũ giáo viên
GD&TĐ - Yếu tố quan trọng làm nên thành công của bộ tài liệu bổ trợ Phát triển năng lực Toán tiếng Anh (I Learn Maths) – sản phẩm thuộc Công ty Cổ phần Giáo dục GMaths - đang thí điểm tại Hà Nội chính là tâm huyết và chất lượng của đội ngũ triển khai.
Lễ ký kết giữa Gmaths và công ty cổ phần Truyền hình Thực tế HDTV
Ngày 30 tháng 06 năm 2019, tại văn phòng Truyền hình Thực tế HDTV Việt Nam đã diễn ra lễ ký kết hợp tác truyền thông triển khai dạy Toán tiếng Anh online và Phát hành tài liệu bổ trợ: Phát triển năng lực toán tiếng Anh - I Learn Maths giữa Công ty cổ phần Truyền hình Thực tế HDTV Việt Nam và Công ty cổ phần Giáo dục Gmaths.